Om eksponentielle funktioner

Definition:

En funktion kaldes eksponentiel, hvis den har en
regneforskrift, der kan skrives således:

f(x) = b·a^x eller y = b·a^x , idet a og b er positive tal.

Eksempel 1:
Indiens befolkning var i 1900 ca. 138 millioner, og er siden
vokset med ca. 2% om året.
Vi siger, at befolkningstallet hvert år fremskrives med 2%.
Den årlige fremskrivningsfaktor er 1,02
Efter 1 år er befolkningstallet: 138 mio ·1,02 = 140,8 mio
Efter 2 år er befolkningstallet: 138 mio ·1,02² = 143,6 mio
Efter 3 år er befolkningstallet: 138 mio ·1,02³ = 146,4 mio
Efter 4 år er befolkningstallet: 138 mio ·1,02⁴ = 149,4 mio
Efter x år er befolkningstallet: 138 mio ·1,02^x

Befolkningstallet kan beskrives med funktionen: f(x) = 138 · 1,02^x
hvor x er antal år efter 1900

Vi lægger mærke til, at befolkningstallet i Indien vokser eksponentielt (med tilnærmelse).
Vi siger, at befolkningstallet kan beskrives med den eksponentielle model:   f(x) = 138 ·1,02^x.

Dette minder meget om kapitalfremskrivning, hvor formlen er: K = K0 · (1+r)ⁿ
Læg mærke til, at n er et helt tal.

I regneforskriften for Indiens befolkning behøver x ikke at være et helt tal.

Eksempel 2:
50g radioaktivt stof, der henfalder med 5% om dagen kan beskrives med en eksponentiel funktion.
Der er en daglig negativ vækst på -5% uanset hvilken dag, der betragtes.
Det er en eksponentielt aftagende funktion og regneforskriften er: y = 50·0,95^x,
hvor x er antal dage siden begyndelsen, da der var 50g.

Bemærk a=0,95, nemlig 1-5% = 1- 0,05 = 0,95


Om a og b
b i regneforskriften kaldes begyndelsesværdien.
Det er fordi, hvis x i regneforskriften b·a^x erstattes med 0, så fås b·a⁰ = b·1 = b

a i regneforskriften kaldes fremskrivningsfaktoren svarende til en tilvækst i x på 1.
Ofte siges blot fremskrivningsfaktoren.
Hvis a er mellem 0 og 1, er funktionen aftagende.
I den eksponentielle model for Indiens befolkning er a = 1,02.
Hver gang, der går ét år, fremskrives Indiens befolkning med 2%.
Man beregner en fremskrivning på 2% ved at gange med 1,02, nemlig den årlige fremskrivningsfaktor.
Den 2-årige fremskrivningsfaktor er 1,02·1,02 = 1,02²
Den 7-årige fremskrivningsfaktor for Indiens befolkning er 1,02⁷

Hvis man kender 2 funktionsværdier y₁ og y₂ , svarende til x-værdierne x₁ og x₂, kan man beregne a ved formlen:


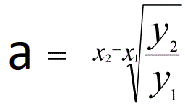
Herefter kan b findes ved hjælp af formlen:
b = y₁ · a^-x₁   eller   b = ^y₁ / _a^x1

(Disse sidste 2 formler giver samme resultat)


Eksempel 3:

Vi betragter 2 funktionsværdier y₁ og y₂ , svarende til x-værdierne x₁ og x₂.



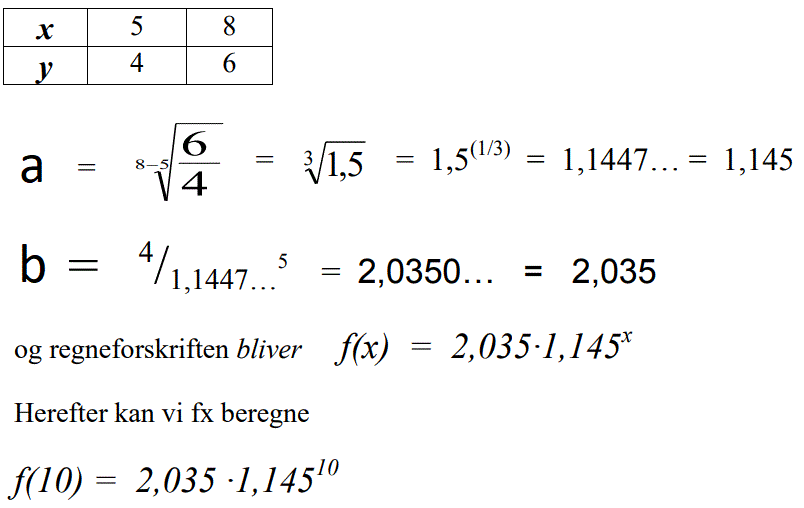
Fordoblings- og halveringskonstant
Ved eksponentielt voksende funktioner tales om en fordoblingskonstant (fordoblingstid) T₂. Det er den forøgelse i x, der giver anledning til en fordobling.
Tilsvarende tales om en halveringskonstant (halveringstid) T_½ ved eksponentielt aftagende funktioner.
Fordoblings og halveringskonstanterne kan ofte aflæses direkte af grafen ved at finde den x-tilvækst, der giver anledning til en fordobling/halvering.
Der gælder følgende formler:



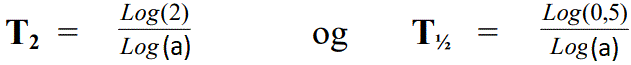
                      Opgaver